THIBAULT LEFEUVRE

Special structures in dynamics and geometry (January 8-10, 25, Jussieu, France)

The first day of the workshop (January 8) will focus on geometry, and it will also be a special occasion to celebrate Uwe Semmelmann’s 60th birthday. The rest of the workshop will concentrate on geometric structures arising in dynamical systems, with a particular emphasis on hyperbolic dynamics and negatively curved geometry.

Room: 15-25 502 (except on Thursday afternoon, room 15-16 413).

Abstracts: see here.

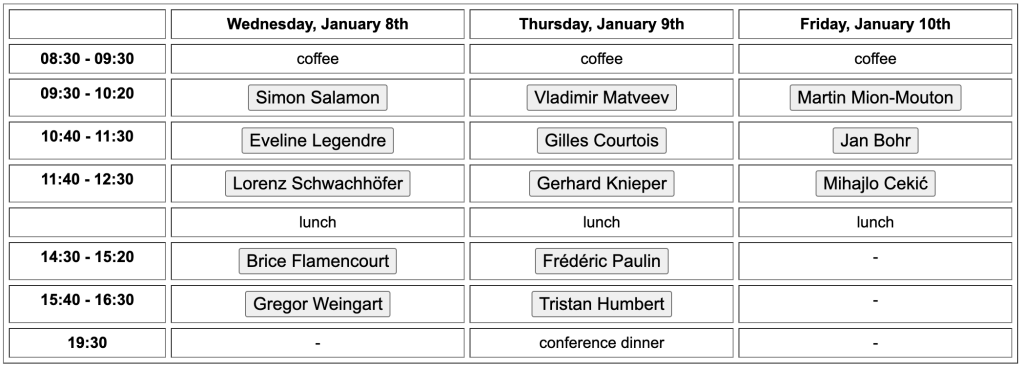
See here for details. For registration, please email one of the two organizers (Andrei or I).

Conférences (passées)

GEOMETRY AND DYNAMICS DAY IN JUSSIEU (DECEMBER 7, 23, JUSSIEU, FRANCE)

On Dec. 7, an extended version of our weekly seminar will take place in Jussieu on the topic Geometry and dynamics. There will be 3 talks (1hr each) and I will defend my HDR in the afternoon.

Zoom link (HDR defense): https://cnrs.zoom.us/j/92968261691?pwd=SHhzTUxKTTdOVEtmSU5uQmJvdW0vdz09

ID de réunion: 929 6826 1691
Code secret: Np3e3w

Schedule:

10-11am: Hamenstädt (room 15/25 502)
11.10am-12.10pm: Pollicott (room 15/25 502)
12.10-2pm: Lunch break
2-3pm: Butt (room 15/16 413, not the same room as the morning session!)
3.30pm: Lefeuvre — HDR defense (room 15/16 413)

Titles and abstracts:

Closed geodesics and stability of negatively curved metrics, Karen Butt.

The marked length spectrum of a closed Riemannian manifold of negative curvature is a function on the free homotopy classes of closed curves which assigns to each class the length of its unique geodesic representative. It is known in certain cases that the marked length spectrum determines the metric up to isometry, and this is conjectured to be true in general. In this talk, we explore to what extent the marked length spectrum on a sufficiently large finite set approximately determines the metric.

The pressure metric on quasi-Fuchsian space, Ursula Hamenstädt.

Thermodynamical formalism can be used to construct a Riemannian (pseudo)-metric on quasi Fuchsian space. We show that this metric has finite diameter. The key point, of independent interest, is the study of positive eigenfunctions on hyperbolic 3-manifolds whose fundamental group is isomorphic to a surface group. This is based on joint work with Elia Fioravanti, Frieder Jaeckel and Yongquan Zhang.

Asymptotic properties of geodesics on flat surfaces, Mark Pollicott.

For closed surfaces of negative curvature ideas from ergodic theory can be used to count (closed) geodesics and to prove natural equidistribution and rigidity results (eg in the work of Margulis and Katok).  We will discuss how some of the results have analogues for flat surfaces (with conical singularities).

WORKSHOP: HYPERBOLIC DYNAMICS AND SEMICLASSICAL ANALYSIS (NOVEMBER 27, 23, JUSSIEU, FRANCE)

This is a one-day long workshop gathering experts in the fields of semiclassical analysis and hyperbolic dynamics. It will take place in Jussieu (Paris, France); there will be 4 talks (1hr each).

Zoom link: https://cnrs.zoom.us/j/93849796537?pwd=V3NaQU5nQXFXdUdCenlnRytMRE9OZz09

ID de réunion: 938 4979 6537

Code secret: fHgDu0

Location: IMJ-PRG, room 15/16 413

Schedule:

10-11am: Leclerc
11.15am-12.15pm: Leclerc
12.15-2pm: Lunch break
2-3pm: Tao
3.15-4.15pm: Chaubet

Titles and abstracts:

Exponential mixing for 3D Anosov flows, Gaétan Leclerc.

The goal of this 2 x 1hr talk is to discuss Masato Tsujii and Zhiyuan Zhang’s paper Smooth mixing Anosov flows in dimension three are exponential mixing (Annals of Maths, 2023). In this very important work, the main difficulty to overcome is (probably) the fact that the « uniform non-integrability condition », that we usually require to prove exponential mixing using Dolgopyat’s estimates, is very difficult to check because of the lack of smoothness of the (strong) stable and unstable foliations. My main goal will be to explain how they overcome this difficulty. We will forget the technicalities in the proofs to only care about the global structure of the paper. We will extract (what I believe are) key arguments, we will discuss them, and we will articulate them together to get a global understanding of this work.

Spectral asymptotics for kinetic Brownian motion on Riemannian manifolds, Zhongkai Tao.

The kinetic Brownian motion is a stochastic process that interpolates between the geodesic flow and the Laplacian. It is an analogue of Bismut’s hypoelliptic Laplacian operator. I will talk about a simple proof of the convergence of the spectrum of kinetic Brownian motion to the spectrum of base Laplacian for all compact Riemannian manifolds without boundary, which generalizes the recent work of Kolb–Weich–Wolf on constant curvature surfaces and is analogous to the theorem of Bismut–Lebeau for hypoelliptic Laplacian. As an application, we prove the optimal convergence rate of kinetic Brownian motion to the equilibrium (given by the spectral gap of the base Laplacian) conjectured by Baudoin–Tardif. This talk is based on joint work with Qiuyu Ren.

Geodesic Levy flights and expected stopping time for random searches, Yann Chaubet.

The narrow capture problem is the study of the time required for a given stochastic process to reach a small target. This problem has been studied extensively for Brownian motion and for other processes, such as Lévy processes (which involve jumps and are therefore discontinuous) in the Euclidean space. In this talk, we will discuss recent results concerning the narrow capture problem on various Riemannian manifolds, and try to explain how the geometry affects the stopping time. This is a joint work with Guedes-Bonthonneau, Lefeuvre and Tzou.

ANALYTIC TECHNIQUES IN DYNAMICS AND GEOMETRY (MAY 28 – JUNE 2, 23, LES DIABLERETS, SWITZERLAND)

Co-organized with Artur Avila, Mihajlo Cekić.

This workshop aims at bringing together mathematicians making use of analytic methods in their study of dynamics, geometry, PDEs, or inverse problems.

In the past twenty years, microlocal and functional analysis techniques have encountered a large success both in hyperbolic dynamics and geometry as they turned out to be ripe enough to tackle unsolved problems in these areas. This development was followed by a number of spectacular results and, on one hand, this workshop aims to celebrate the success of such methods by bringing together the leading specialists. On the other hand, its goal is to serve as a fertile environment for the advancement of analytic methods in more complicated dynamical systems, such as partially hyperbolic or parabolic, by gathering the pioneers in these areas at one place and spurring a novel exchange of ideas between experts in analysis and dynamics. Topics should include:

• the theory of Pollicott-Ruelle resonances and transfer operators in hyperbolic dynamics;
• analytic methods in non-hyperbolic dynamics (frame and horocycle flows, for instance);
• geometric inverse problems;
• scattering resonances, spectral rigidity, quantum ergodicity, or semiclassical phenomena.

IMJ-PRG summer school : Microlocal and probabilistic methods in dynamics and geometry (JULY 3-7, 23, CAMPUS DE JUSSIEU)

Co-organized with Mihajlo Cekić, Oana Ivanovici, Frédéric Naud.

Microlocal analysis and probabilistic methods have encountered a large success in the past decade, both in hyperbolic dynamics and in geometry. These developments led to a number of spectacular results and, on one hand, this summer school aims to celebrate the success of such methods by bringing together the leading specialists as well as the young researchers starting their career in these fields. On the other hand, its goal is to serve as a fertile environment and to provide young participants with the state-of-the-art analytic and probabilistic techniques used in geometry and dynamics.

Deadline for registration: 28/02/2023

---